2.2 Tight-binding
Featured work
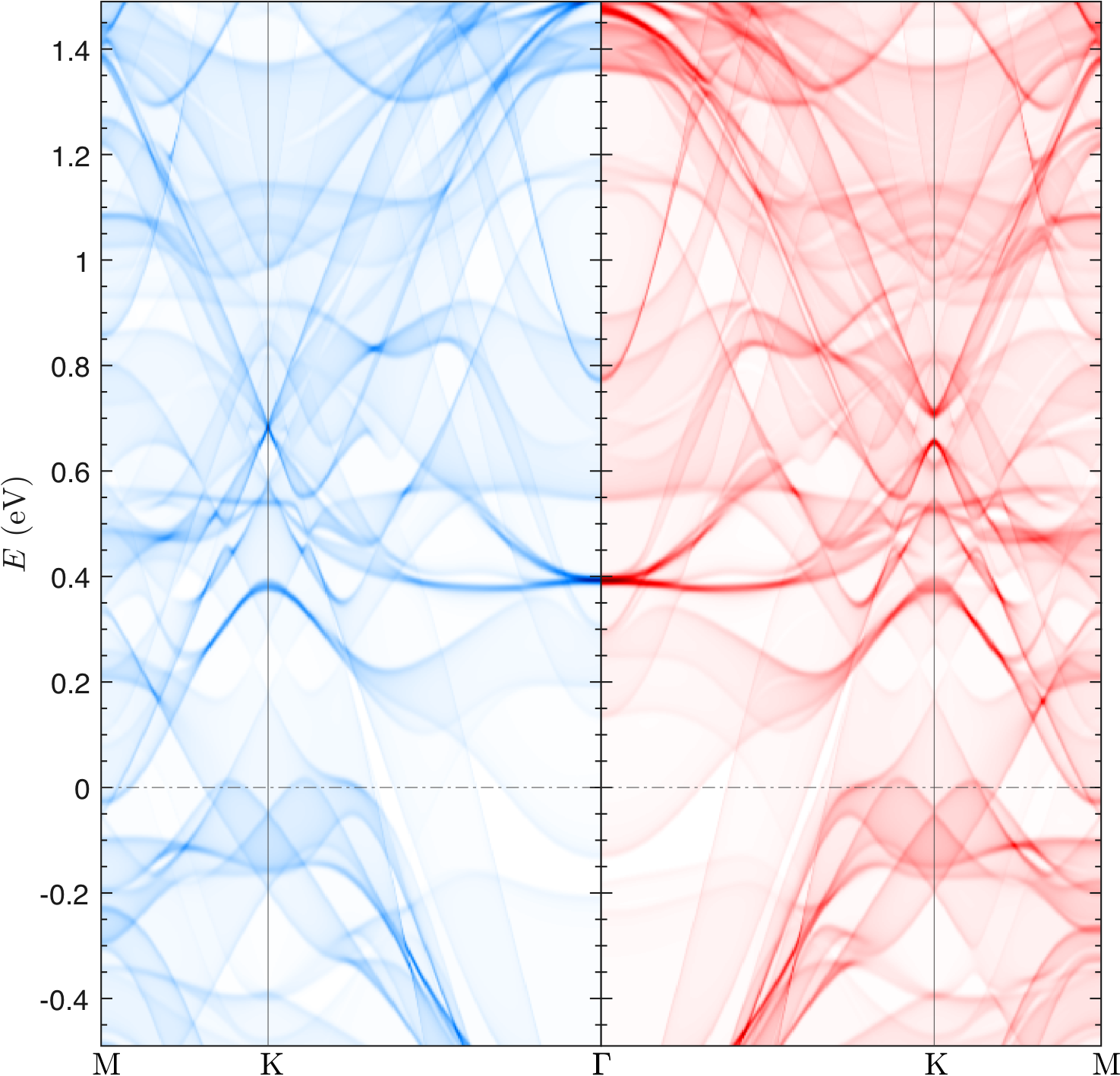
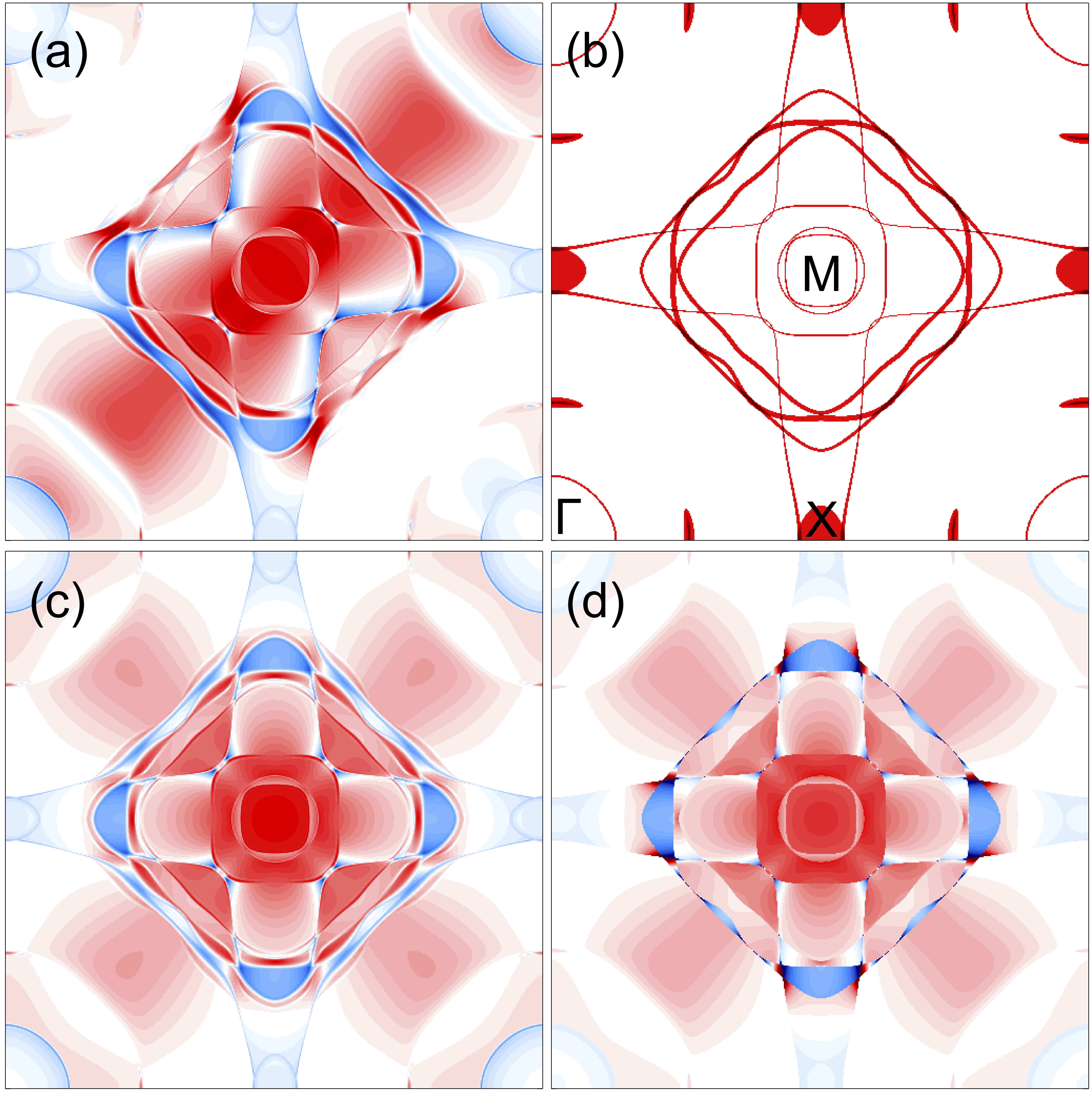
Figure 2.2: Left: The band structures projected on surface BZ near the Fermi level in TbMn\(_6\)Sn\(_6\). Right: \(k\)-resolved MAE and Fermi surface contour in CoPt for \(k_z=0\) calculated in TB. Red (blue) color indicates positive (negative) contributions to MAE. (a) \(k\)-resolved MAE calculated via the magnetic force theorem. (b) Fermi surface contour plot. (c) Symmetrized \(k\)-resolved MAE. (d) Symmetrized \(k\)-resolved MAE calculated via perturbation theory.
Interplay between magnetism and band topology in Kagome magnets \(R\)Mn\(_6\)Sn\(_6\)
Y. Lee and R. Skomski and X. Wang and P. P. Orth and A. K. Pathak and B. N. Harmon and R. J. McQueeney and Liqin Ke
arxiv (2022)
Intersublattice magnetocrystalline anisotropy using a realistic tight-binding method based on maximally localized Wannier functions
Liqin Ke
PRB 99, 054418 (2019)
TB has the advantage of speed and the clarity of interpretation. Starting from the realistic TB Hamiltonain, based on the Wannier90 technique or other non-orthonormalized TB basis, this code can be used to explore electronic and magnetic properties.
Features and Capabilities
- Bandstructure, spectra functions, Fermi surface
- Green’s functions (GF)
- Spin-orbit coupling (SOC)
- Perturbation theory treatment of SOC using GF
- Pairwise exchange coupling and magnetocrystalline anisotropy using linear response
- Orthogonal and non-orthogonal basis
Brief descriptions
Spectral function
To better illustrate the \(k_z\) dependence of band structures in bulk layered materials, we project all bands onto the surface BZ by integrating the \({\bf k}\)-dependent spectral function, over \(k_z\), \[\begin{equation} I({\bf k}_{\parallel},\omega) =\int_{0}^{1} \mathrm{d}k_z\ \sum_i \delta[\omega-E_i({\bf k}_{\parallel}, k_z)]. \label{eq:DOS_projected} \end{equation}\] Here, \(k_z\) is integrated from 0 to 1 r.l.u., while \({\bf k}_\parallel\) is in the basal plane.Pairwise magnetocrystalline anisotorpy
\[\begin{equation} K =\sum_{ij,\sigma\sigma'} \widetilde{K}_{ij}^{\sigma\sigma'} \label{eq:kprime} \end{equation}\]
\[\begin{equation} \widetilde{K}_{ij}^{\sigma\sigma'} = -\frac{2}{\pi}\operatorname{Im}\int_{-\infty}^{\epsilon_\text{F}}\,\mathrm{d}\epsilon\int\,\mathrm{d}{\bf k} \mathop{\mathrm{Tr}}\left[ G_{ij}^{\sigma}({\bf k},\epsilon)U_{j}^{\sigma\sigma'}G_{ji}^{\sigma'}({\bf k},\epsilon)A_{i}^{\sigma^\prime\sigma}\right]. \label{eq:k2} \end{equation}\]
Here, \(U\) and \(V\) are the isotropic and anisotropic parts of the spin-orbit-coupling potential: \[\begin{align} \begin{split} 2U &= V(\hat{\bf n}_{110})+V(\hat{\bf n}_{001}) \\ 2A &= V(\hat{\bf n}_{110})-V(\hat{\bf n}_{001}). \end{split} \end{align}\]
- Others
Relevant publications: