2.3 Spinwave theory

Featured work

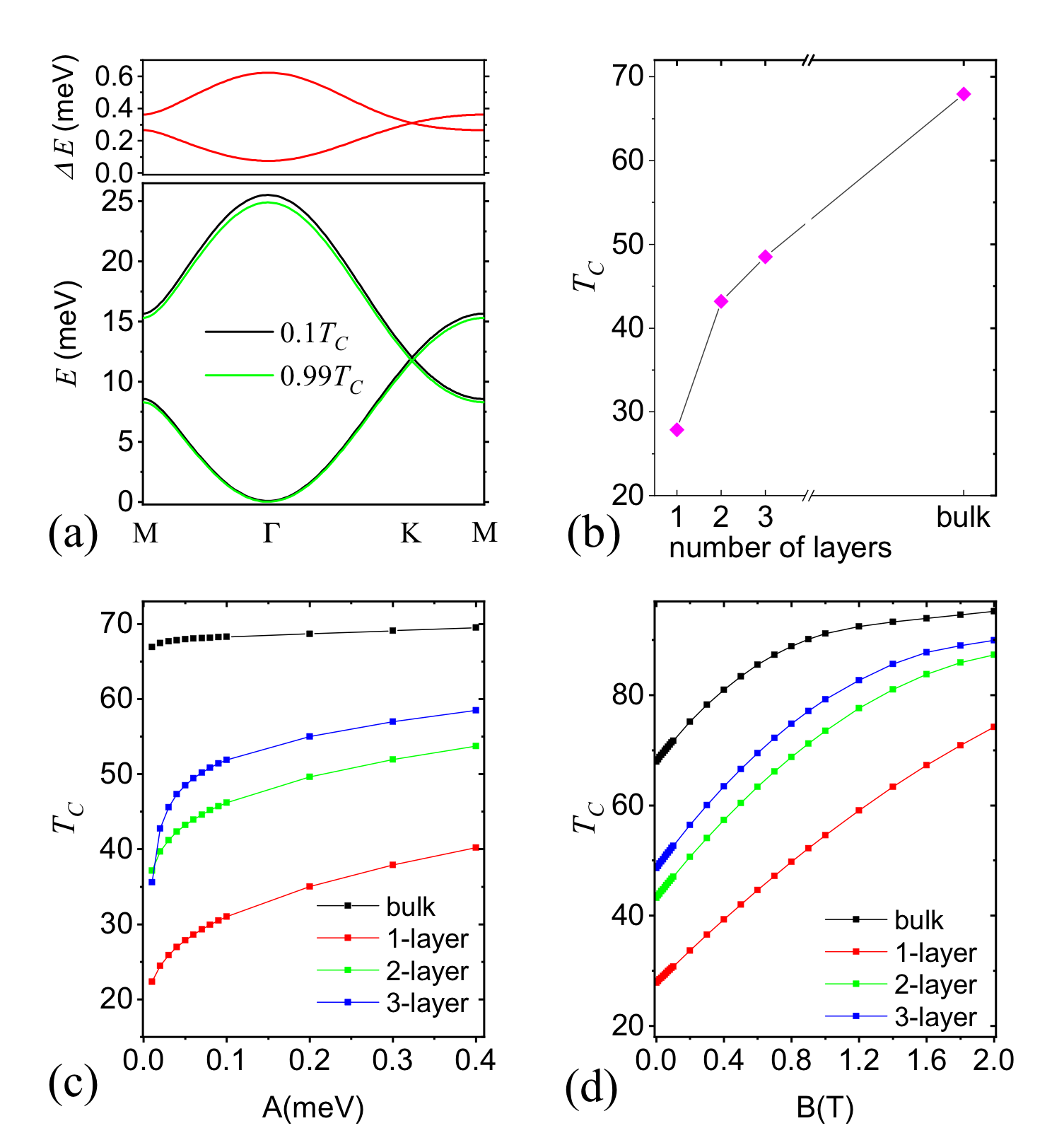
$SRSWT results for Cr$_2$Ge$_2$Te$_6$. (a) Renormalized spin-wave spectrum of the monolayer at temperatures $0.1T_C$ and $0.99T_C$ is plotted with black and green lines in lower panel. The difference of the black and green lines, $\Delta E$, is plotted in upper panel. (b) Layer dependence of the critical temperature. Strong dimensionality effect is observed from 2D to bulk, with critical temperature ranging from about $27.8$K to $68$K. (c) Single-ion anisotropy dependence of the critical temperature at zero magnetic field. In low dimensions, critical temperature sensitively depends on the value of anisotropy. (d) Magnetic field dependence of the critical temperature, at single-ion anisotropy $A=0.05$~meV. The non-zero value of $A$ cuts off the sharp dependence of $ c$ on $B$ at the low-field side.$

Figure 2.3: SRSWT results for Cr$_2$Ge$_2$Te$_6$. (a) Renormalized spin-wave spectrum of the monolayer at temperatures $0.1T_C$ and $0.99T_C$ is plotted with black and green lines in lower panel. The difference of the black and green lines, $\Delta E$, is plotted in upper panel. (b) Layer dependence of the critical temperature. Strong dimensionality effect is observed from 2D to bulk, with critical temperature ranging from about $27.8$K to $68$K. (c) Single-ion anisotropy dependence of the critical temperature at zero magnetic field. In low dimensions, critical temperature sensitively depends on the value of anisotropy. (d) Magnetic field dependence of the critical temperature, at single-ion anisotropy $A=0.05$~meV. The non-zero value of $A$ cuts off the sharp dependence of $ c$ on $B$ at the low-field side.

Self-consistently renormalized spin-wave theory of layered ferromagnets on the honeycomb lattice
V. V. Mkhitaryan and Liqin Ke
PRB 104, 064435 (2021)

Features and Capabilities

Temperature-dependent magnetization and spinwave spectra, and critical temperatures for low-dimension magntic systems
Disorder effects on spinwave spectra

Brief descriptions

Starting from a classical Heisenberg-type Hamiltonain, including isotropic exchange coupling, magnetocrystalline anisotropy, and DMI terms, this code calculate the spin wave in both linear spinwave theory and nonlinear spinwave theory.

Self-consistently renormalized spin-wave theory

We develop a self-consistently renormalized spin-wave theory, within a mean-field approximation, for the two-dimensional Heisenberg ferromagnet with perpendicular easy-axis anisotropy on the honeycomb lattice, as well as its few-layer and bulk extensions. In this method, the magnetization dependence on temperature is found as the solution of the self-consistency equation. Furthermore, we account for the physical difference of surface and bulk layers by treating the layers as separate sublattices. Thus the method can be readily generalized to study various magnetic phenomena in a broad range of systems, including those comprising magnetically inequivalent sublattices. Using our theory, we calculate the temperature-dependent magnetization for two chromium-based layered van der Waals insulating magnets, Cr$_2$Ge$_2$Te$_6$ and CrI$_3$, employing various sets of Heisenberg exchange and single-ion anisotropy values reported for these materials in the existing literature. As expected, we observe a strong dimensionality effect where the ordering temperature is reduced and its sensitivity on the anisotropy is enhanced with the decrease of dimensionality.

Disorder effects
Others

(Mkhitaryan and Ke 2021)

Publications

Mkhitaryan, V. V., and Liqin Ke. 2021. “Self-Consistently Renormalized Spin-Wave Theory of Layered Ferromagnets on the Honeycomb Lattice.” Phys. Rev. B 104: 064435. https://doi.org/10.1103/PhysRevB.104.064435.