1.1 2D van der Waals materials

Two-dimensional (2D) quantum materials offer potential novel applications in energy-efficient, nanoscale information storage and computing. The intimate interplay between correlated electrons, lattice, and magnetism can result in a rich variety of interesting and important physical phenomena. In two-dimensional (2D) materials with open $d$- or $f$-shells, additional quantum confinement caused by the reduced dimensionality suppresses the screening, and thus may further enhance the electron correlation. The recent development of magnetic 2D van der Waals (vdW) materials adds a new magnetic functionality to the already vast appeal of the 2D materials family. Their magnetism is very sensitive to, and can be controlled by, pressure, stacking arrangement, and external magnetic and electric fields. Such tunability offers opportunities to design and construct new energy-efficient spin-based devices. Even in their bulk form, the reduced coordination number in quasi 2D lattices constrains the electron hopping, thereby increasing the role of the Coulomb interaction. The resulting enhancement of electron correlations directly affects exchange interactions. The critical question is how the magnetic excitations in these confined systems can be understood, controlled, and exploited.

Electron correlation effects on exchange interactions and spin excitations in 2D van der Waals materials
Liqin Ke and Mikhail I. Katsnelson
npj Comput Mater 7, 4 (2021)

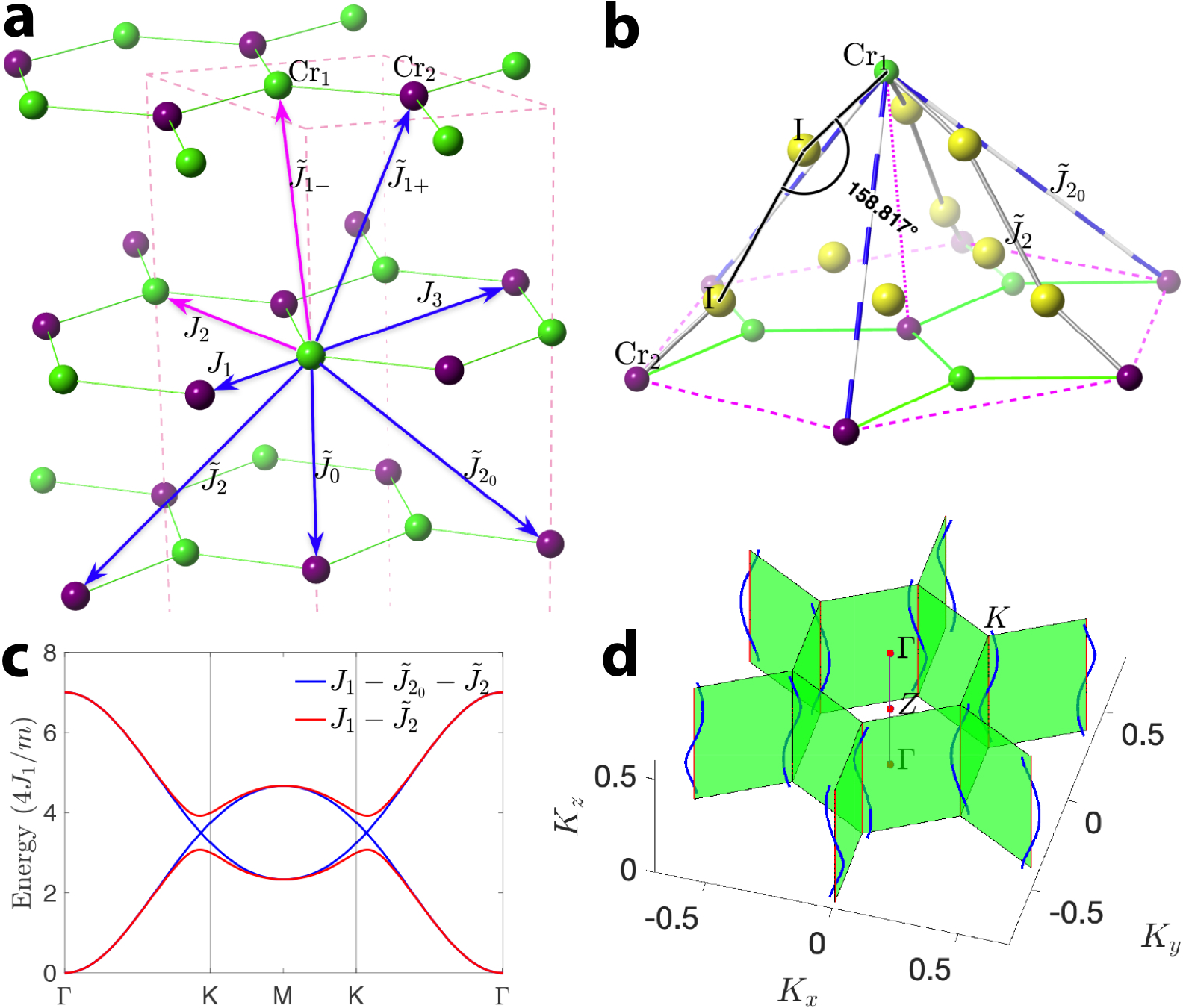
$\textbf{Exchange parameters, SW spectra and nodal lines calculated using linear spinwave theory.} \textbf{a} Pair exchange parameters for the first few neighbors in R-CrI$_3$. \textbf{b} Atomic configurations around the exchange paths of $\tilde{J}_{2_0}$ and $\tilde{J}_2$. AFM $\tilde{J}_{2}$ corresponds to a Cr-I-I-Cr super-superexchange coupling. \textbf{c} SW spectra along the $\Gamma$--$K$--$M$ path calculated within a $J_1$--$\tilde{J}_{2}$--$\tilde{J}_{2_0}$ ($\tilde{J}_{2}=\tilde{J}_{2_0}={J}_{1}/12$) model and a $J_1$--$\tilde{J}_{2}$ ($\tilde{J}_{2}={J}_{1}/6$) model. \textbf{d} Dirac nodal lines, where the magnon bands cross, wind around the $K$-point and along the $\hat{k}_{z}$ direction; the exchange parameters calculated in QSGW$+U$ are used.$

Figure 1.1: Pair exchange parameters for the first few neighbors in R-CrI$_3$. Atomic configurations around the exchange paths of $\tilde{J}_{2_0}$ and $\tilde{J}_2$. AFM $\tilde{J}_{2}$ corresponds to a Cr-I-I-Cr super-superexchange coupling. SW spectra along the $\Gamma$–$K$–$M$ path calculated within a $J_1$–$\tilde{J}_{2}$–$\tilde{J}_{2_0}$ ($\tilde{J}_{2}=\tilde{J}_{2_0}={J}_{1}/12$) model and a $J_1$–$\tilde{J}_{2}$ ($\tilde{J}_{2}={J}_{1}/6$) model. Dirac nodal lines, where the magnon bands cross, wind around the $K$-point and along the $\hat{k}_{z}$ direction; the exchange parameters calculated in QSGW$+U$ are used.

2022 (Liu et al. 2022; Lee et al. 2022)
2021 (Ke and Katsnelson 2021; Lee et al. 2021; Mkhitaryan and Ke 2021; Gordon et al. 2021)
2020 (Lee, Kotani, and Ke 2020)
2019 $\ge$ (Ke 2019)

Publications

Gordon, Elijah, Vagharsh Mkhitaryan, Haijun Zhao, Yongbin Lee, and Liqin Ke. 2021. “Magnetic Interactions and Spin Excitations in van Der Waals ferromagnet VI$_3$.” Journal of Physics D: Applied Physics. http://iopscience.iop.org/article/10.1088/1361-6463/ac1bd3.

Ke, Liqin. 2019. “Intersublattice Magnetocrystalline Anisotropy Using a Realistic Tight-Binding Method Based on Maximally Localized Wannier Functions.” Phys. Rev. B 99: 054418. https://doi.org/10.1103/PhysRevB.99.054418.

Ke, Liqin, and Mikhail I Katsnelson. 2021. “Electron correlation effects on exchange interactions and spin excitations in 2D van der Waals materials.” Npj Computational Materials 7 (4): 1–8. https://doi.org/10.1038/s41524-020-00469-2.

Lee, Y., V. N. Antonov, B. N. Harmon, and Liqin Ke. 2021. “X-ray spectra in the magnetic van der Waals materials ${\mathrm{Fe}}_{3}\mathrm{Ge}{\mathrm{Te}}_{2},$ ${\mathrm{CrI}}_{3}, \mathrm{and} \mathrm{Cr}\mathrm{Ge}{\mathrm{Te}}_{3}$: A first-principles study.” Phys. Rev. B 103: 134407. https://doi.org/10.1103/PhysRevB.103.134407.

Lee, Y., Takao Kotani, and Liqin Ke. 2020. “Role of nonlocality in exchange correlation for magnetic two-dimensional van der Waals materials.” Phys. Rev. B: Rapid Communication 101: 241409. https://doi.org/10.1103/PhysRevB.101.241409.

Lee, Y., R. Skomski, X. Wang, P. P. Orth, A. K. Pathak, B. N. Harmon, R. J. McQueeney, I. I. Mazin, and Liqin Ke. 2022. “Interplay between magnetism and band topology in Kagome magnets $R$Mn$_6$Sn$_6$.” arXiv 2201 (May): 11265.

Liu, Yu, Myung-Geun Han, Yongbin Lee, Michael O. Ogunbunmi, Qianheng Du, Christie Nelson, Zhixiang Hu, et al. 2022. “Polaronic Conductivity in Cr$_2$Ge$_2$Te$_6$ Single Crystals.” Advanced Functional Materials 2022: 2105111. https://doi.org/https://doi.org/10.1002/adfm.202105111.

Mkhitaryan, V. V., and Liqin Ke. 2021. “Self-Consistently Renormalized Spin-Wave Theory of Layered Ferromagnets on the Honeycomb Lattice.” Phys. Rev. B 104: 064435. https://doi.org/10.1103/PhysRevB.104.064435.